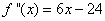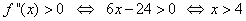MATH HOMEWORK HELP

17. Given, on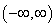

(a) Find the critical numbers of the first-order

Solution: We compute the first derivative, and set it equal to zero

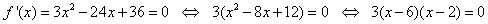
Hence, the critical points areand.

(b) Find the intervals of increase and decrease. Show work that supports conclusion

Solution: The derivative is equal to

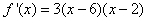
• The function is increasing if

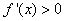
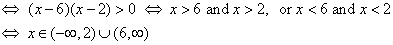
• The function is decreasing if

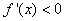
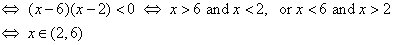
(c) Give the coordinates of the local maximum, if any

Solution: We find the second derivative

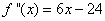
• . This means that is a local maximum

Therefore, the coordinates of the local maximum is (2, 37).

(d) Give the coordinates of the local minimum, if any

Solution: Similarly

• . This means that is a local minimum.

Therefore, the coordinates of the local maximum is (6, 5).

(e) Find the intervals on which f(x) is concave up and the intervals on which it is concave down. Show the work. Find the coordinates of the inflection point, if there is any

Solution: We already calculated the second derivative

• Concave up: